p
i
c
t
u
r
e |
Spring Break!
(07 Mar 2005 at 21:23) |
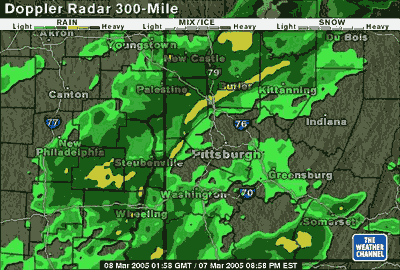 Based on this image, I decided not to go to hockey tonight, even though it not raining right this instant. This storm has been encircling us ominously all day, and the hockey instructors have a bad habit of cancelling only after we've taken the trouble to actually drive out there. Let's hope I'm right!
After a small type-theoretic victory last week, I'm back to proving theorems in Twelf. This should be easier now that my "theorems" are not known to be false. I still want to be writing a proposal by the end of the semester, since everyone around me seems to be doing that, or at least graduating.
I am still addicted to hacking on escape. Rather than fixing certain obvious deficiencies (sound, solution sharing, editor cut-and-paste), I have been making large changes to the gameplay by adding in robots of various sorts. I think robots will compound the fun factor polynomially, he said, which, to his delignt, causes cringes in those who hate idea that mathematics and fun could possibly be associated, deliberate and delightful in the same way as doing type theory in a bar. |  |
|
I didn't know there was a Palestine in Pittsburgh's neighborhood! And a Washington. How many Washingtons would there be in America?
And did it rain yet? |
Nearby we also have "Edinboro" (pronounced phonetically) and "Versailles" (also pronounced phonetically!) There's probably a Washington and a Springfield in every state.
It did eventually rain, though not as hard as I thought it would. |
| Premises go above the bar, conclusions below it, and ridiculous ideas go in it. |
Here's a question for hardcore Twelf fans, assuming some might be reading this:
Is it accurate to say that proving things in Twelf always means writing logic programs? If so, doesn't this bring you much more pain than it's worth, compared to tactic-based theorem provers? Do you think a Twelf expert will be as or more efficient at proving complex theorems as a Coq expert? |
There is also a theorem prover in twelf, which, given a goal, sometimes comes up with (what is really a logic program) proof of that goal.
There is a general question you seem to be asking an instance of. It's "In technique A I must create Xs "by hand", and in technique B I use some tools to create them "automatically". Isn't technique B clearly superior?"
While I don't doubt that, all other things being equal, computers automating more things is great, it seems like there are some costs to worry about. (I haven't actually had a lot of experience with Coq or other tactic-based provers, so I'd love to hear about your experience using them)
If the relevant tactics are specific, then I may suffer a "thinking cost" in how to phrase my informal proof in terms of those tactics, just as I have to think about how to phrase it in terms of twelf logic programs.
If the relevant tactics are very general, (like, a single TRY-TO-PROVE-USING-BRILLIANT-INSIGHT tactic) then I may suffer a performance cost in the machine trying to figure out how to apply the tactic in order to get a proof. I
If the tactics change over time, then there's a maintenance problem to be dealt with or at least worked around, in that a proof script that worked in the past no longer works with the modified tactics. I've heard rumors that this has been a problem with OTTER, but I don't know how accurate they are.
Anyway, after thinking about it for a bit, I'm sympathetic to the idea that representing proofs as hand-coded logic programs is certainly not the single most natural way of formalizing proofs. However, just like arguments about "expressiveness" and "naturalness" of programming languages, I don't know how to evaluate claims that a particular tactic-based system has a better set of building blocks. If you look past direct human use of the twelf metaproving system, its mathematical cleanliness has some benefits in terms of other programs manipulating and proving things about its structures. It might be rather hard to show that some particular tactic, say, terminates, but given the style of the algorithms that twelf uses, I imagine it would be rather easier there to prove such properties. |
I don't know much about Coq, so I can't compare the two systems. Do I remember right that you don't get higher order abstract syntax as an encoding and reasoning tool "for free"? If so, that would be a major problem for the kind of work I'm doing.
Twelf proofs are a kind of logic program, yes. It's actually a fairly natural way of capturing the reasoning that I do when proving things on paper, which is nice. I don't see why that would be any trouble, more or less than it is worth. A functional language would perhaps be better still, and I think this is seen as one of the future directions for Twelf in the community (ie Delphin).
I use Twelf to prove things, and I prove things both to assure myself that they are true, and to understand why they are true (or, understand why not, when they aren't). Doing proofs by hand certainly helps me to understand the structure of the proof and diagnose problems (or form new ideas), at the cost of, well, doing the work of proving things by hand.
If I were just trying to get proofs of theorems, or test their validity, automated theorem proving (perhaps using tactics) would probably be expedient. Like Jason said, unless you have a clear specification of when the theorem proving will be successful, I do worry about issues of maintainability over time. I think really writing down the proofs by hand is superior in this regard. |
| So fitting to see a radar image in Tom 7 Radar. |
| So fitting to see Jcreed and Tom7 break into conversation that I don't begin to understand on Tom 7's Radar! |
| Impossible! Everything I say is perfectly and immediately gomburgible. |
| Your search - gomburgible - did not match any documents. |
| Did you mean... hamburgler? |
I've used Coq to prove soundness of TALx86 for our local Foundational PCC system. From what I've heard of other efforts that use Twelf, it seems like this was measurably more pleasant.
About the "thinking cost": When you want to prove something about arithmetic that you would say is "obvious" in an informal proof, it sure is nice to invoke the tactic for the Omega procedure, instead of writing a logic program. :-) This is an example where I think everyone agrees that the thinking would be a bad use of time.
Also, in the context of mobile code security, you focus more on a small TCB for the end-user, so it's sort of inconsequential whether anyone "understands" a proof that a system is sound, modulo issues of revising the proof due to changes in the system. For the same reason, we don't worry overly much about the performance costs of tactics, since each tactic produces an efficiently-checkable standalone proof in the end. Similarly for the question of whether tactics terminate.
For mature systems like Coq, the tactics aren't changed in backwards-compatibility-breaking ways. When they recently changed the syntax, they included a translator from the old syntax, and my old proofs worked in the substantially refactored new version without manual intervention.
It's true that you can't use higher-order abstract syntax with Coq. The reason is based on the neat result that, while simply-typed lambda calculus is strongly normalizing, it becomes Turing complete-ish when you add the simplest formulation of recursive types. Coq uses syntactic restrictions to keep the calculus strongly normalizing, even with recursive types. I think this is morally equivalent to the Twelf totality checker, and it seems to me to be better integrated into the core logic. There is no way to type-check a Coq function definition if the function isn't total, for instance, even though you can basically use the complete functional subset of OCaml in such definitions.
I use hand-rolled syntactic substitution in place of higher-order abstract syntax. The added cost is basically just defining a substitution function, figuring out what lemmas I need about it, and what inductive hypotheses I need for their proofs. The proofs themselves are automated. |
I can't help but agree with you about arithmetic. Soooo boring to prove those theorems by hand.
I really should play with Coq some, to see whether I miss much in the way of HOAS. Already to formalize a lambda calculus where beta-normal eta-long forms are maintained syntactically (due to Kevin Watkins) you kind of have to do an amount "real work" to define substitution even in twelf that's roughly proportional to how complicated your syntax is.
|
Yeah, I think those are fair criticisms. But anyway, like I said, the way I use it isn't to produce machine-checkable proof certificates, but to work the problem in a very detailed way, with help from the computer. (It would be great, though, if Twelf could output certificates for its totality checking!)
I must misunderstand something you're saying, though--how is it that Coq allows you to use the "complete functional subset of O'Caml" but that you can't do HOAS? One can certainly do HOAS in ML. Is it that you kist can't induct over the things afterwards? |
"Do you think a Twelf expert will be as or more efficient at proving complex theorems as a Coq expert?"
It depends on what you are doing. Twelf gives you certain substitution lemmas for free. If you aren't using those, you are probably better off using Coq, simply because it is a bit more mature, so there are more libraries, more automation, etc.
"Doing proofs by hand certainly helps me to understand the structure of the proof and diagnose problems"
You can always write explicit proof terms in Coq, and I know somebody who prefers to do this. (You are writing a functional, not a logic program, but this is mostly a matter of syntax, given that Twelf, I believe, internally translates the logic program into a functional one.)
"Like Jason said, unless you have a clear specification of when the theorem proving will be successful, I do worry about issues of maintainability over time. I think really writing down the proofs by hand is superior in this regard."
You can get the explicit proof term generated by a tactic, if you are worried about tactics changing over time. I've found that automation is nice because it makes your proofs more robust with regards to small changes in your system. With tactics, your proofs will still sometimes break, but without them, they will always break.
"One can certainly do HOAS in ML."
Sort of, but you can't really go under the lambda except in a very limited fashion. |
So my statement about "the functional subset of OCaml" was inaccurate. In my defense, I did preface it with the get-out-of-jail-free-card "basically." :-)
What I really meant is that you can use the basic ML syntax that you're used to instead of having to express all recursion as calls to fold functions, or otherwise indicating primitive recursion explicitly.
In response to Andrew: I'm still not convinced that substitution lemmas alone make Twelf worth using. An arithmetic decision procedure is such a time saver for proving facts about assembly programs. Coq also has a bag of other very useful tactics, including one that uses a complete propositional logic decision procedure (combined with definition unfolding and other low-cost tactics) to solve as much of a goal as it can and then decompose the rest into simplified subgoals. |
As I said, it depends on what you are doing. For something like assembly, with lots of arithmetic and little substitution, I think Coq is a lot better.
Also, there is no reason Twelf cannot have an arithmetic decision procedure, whereas there is a reason Coq cannot have HOAS, but your query seems more pragmatic than that. |
| In fact, Twelf does already have constraint domains for integers (and soon, I believe, integers-modulo-2^n), although the coverage checker currently doesn't work on these. |
|
|
|
|