p
e
r
s
o
n
a
l |
Pac Tom September update
(12 Sep 2010 at 00:26) |
Time for another update on my project to run the length of every street in Pittsburgh, called Pac Tom. It's all about the map:
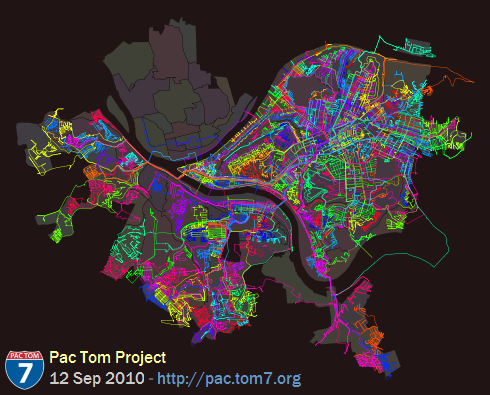
Also available is the same map in PDF so that you can pinch to zoom. Over on the right (known to cartographers as "East") you can see Pac Tom Level 1, totally all done. I've been hard at work on the stuff South of the Monongahela since I finished Level 1 almost two years ago. It's hard because it's far from my house (see rules and regulations) and crazy hilly. You can see that I've made a lot of progress either just by the superbrite color lines all over everything (btw that image above is about 136 square miles, about 140 feet per pixel) which is where I went, or by comparing to last time, or by me being more specific:
Neighborhoods totally done (level 2): Banksville, Beltzhoover, Bon Air, Brookline, Carrick, Chartiers City, East Carnegie, Esplen, Fairywood, Hays, Knoxville, Lincoln Place, Oakwood, Overbrook, Ridgemont, St. Clair, Westwood, Windgap.
Total running events (this includes Pac Tom, training, races, and 3D World Runner): 734
Total time recorded: 25 days, 23:15:38
Total distance: 4230.118 miles
But actually what I really wanted to show you was a newer map, which has been on the Pac Tom site for a while but I have never explained. It's the shortest paths map:

Well, at this view it just looks like the regular map vomited a rainbow all over itself. What's going on is that this is a graph of all of the places I've been (each individual GPS waypoint), connected by heuristics (like they were consecutive in a trip, so I actually ran between them, or they appear to be near enough to imply that I could run between them) and then I compute the shortest path from each point back to my home. Here's a zoom up:
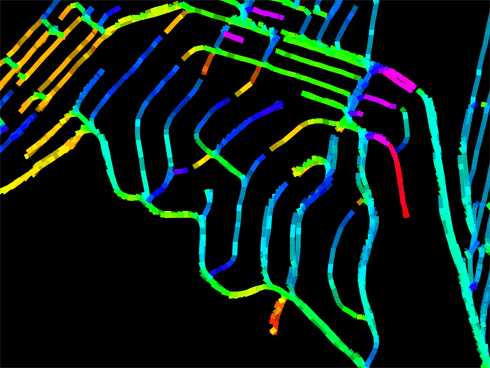
Bonus points if you recognize the neighborhood! See all those fingersnakes reaching up to meet one another? Those aren't dead ends, they're the farthest away from my house I can get on those roads (the leaves in the minimal spanning tree rooted at my house). On one side, the shortest path is to go South, but just a few feet away, the shortest way is to go North. (My house is Southeast from here.) I spent a lot of (fun) time writing this code partly in the hopes that it would teach me about better ways to get out to distant neighborhoods, but it turns out that on city streets (especially grids), the shortest path on foot is usually pretty obvious. Even when it's not, the difference rarely exceeds 100 feet. The most interesting places are probably choke points, like bridges:
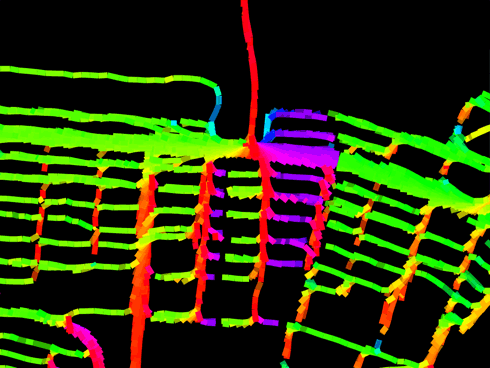
Pretty much everything nearby points up this bridge. The colors by the way are not gratuitous; they indicate the physical heading that I should be running on that segment to decrease my distance to home. Green means East, red means North, violet means West, cyan means South. This is meant to emphasize the break-even points described above. Here you can see from the thickness of the lines (which just comes from having lots of runs through there, with GPS noise) that I don't usually take the Birmingham Bridge, even though it would save me about a South Side block's width (that's the pink stuff: Turn around!) I usually prefer the Hot Metal Bridge to the East because it's got better pedestrian access and also my brain autopilot is accustomed to the area, having run it like a hundred times. Unfortunately it's hard to get route preferences (and other stuff like elevation change) incorporated into the formulas. So, rainbow brite indeed but not actually that useful. The maps are updated automatically after every run onto the graphics page. You can check out the source code which of course is mostly calls out to general-purpose libraries for loading GPS data and computing fine-grained distances on the earth pear's surface and undirected graphs and snapping the neighborhood boundaries to be exactly perfect, and outputting the SVG, all of which I of course wrote myself even though it probably or certainly already exists because have you MET Tom? |  |
 |
FINAL BOSS:
FRANK PFENNING SQUASH BATTLE
BALL IS ACTUALLY A NUKE |
I still never sleep
humor quality goes way way down |
| is the bathroom mushroom thread kindof like a bathroom mushroom itself? |
| Sally matus the final boss is racing Bob Harper on a bike through the dirty dozen. |
oh that boss has a glitch.
just assert the superiority of haskell to ML in some way, and he runs out of breath. |
 |
|
|
|